洛谷《P1126》题解

题面

题目描述

机器人移动学会（RMI）现在正尝试用机器人搬运物品。机器人的形状是一个直径1.6米的球。在试验阶段，机器人被用于在一个储藏室中搬运货物。储藏室是一个 N×M 的网格，有些格子为不可移动的障碍。机器人的中心总是在格点上，当然，机器人必须在最短的时间内把物品搬运到指定的地方。机器人接受的指令有：向前移动1步（Creep）；向前移动2步（Walk）；向前移动3步（Run）；向左转（Left）；向右转（Right）。每个指令所需要的时间为1秒。请你计算一下机器人完成任务所需的最少时间。

输入格式

第一行为两个正整数_N,M(N,M ≤ 50)，下面_N_行是储藏室的构造，0表示无障碍，1表示有障碍，数字之间用一个空格隔开。接着一行有4个整数和1个大写字母，分别为起始点和目标点左上角网格的行与列，起始时的面对方向（东E，南S，西W，北N_），数与数，数与字母之间均用一个空格隔开。终点的面向方向是任意的。

输出格式

一个整数，表示机器人完成任务所需的最少时间。如果无法到达，输出-1。

img

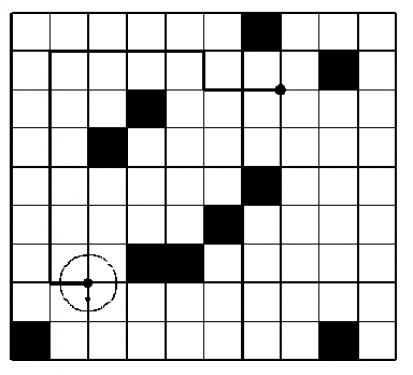
输入输出样例

输入

1
2
3
4
5
6
7
8
9
10
11
9 10
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0
7 2 2 7 S

输出

1
12

思路

注意点

  • 首先，这道题需要注意：障碍物在格子上的，但是机器人是在交叉点上走路的。某人自信的写完代码后（就是我）写完代码后发现题读错了。
  • 那么还要注意到的地方是起点和终点是可能重合的，需要特殊处理；起点也可能是障碍物，也要做特殊处理。
  • 还有要注意到的是，对于每一步，你走一个格点，两个格点或三个格点所耗时间都是1，不要搞乱；而每转90°，也要耗一定时间，所以千万要小心。
  • 注意机器人是球形且有直径，所以机器人并不能到达储藏室的边缘。
  • 注意在移动时机器人也需要一步一步移动，所以机器人不能跨过障碍物，即遇到障碍物就必须停止。

所需变量

1
2
3
4
5
int fx[5]={0,-1,1,0,0}; 
int fy[5]={0,0,0,-1,1};
int ft[5]={0,1,4,2,3};
int fft[5]={0,1,3,4,2};
int abc[5]={0,1,2,1,0};

fx[i]表示方向i(编号)的x的进退情况 。

fy[i]表示方向i(编号)的y的进退情况 。

ft[i]表示顺时针排列各个方向的编号(上1 右4 下2 左3) 。

fft[i]表示数字i在ft[]数组中的下标 。

abc[5]表示转到[顺时针转i次到达的那个方向]的最短次数 。

其中ft数组和abc数组比较难理解

下面我们逐个讲讲

abc数组

1
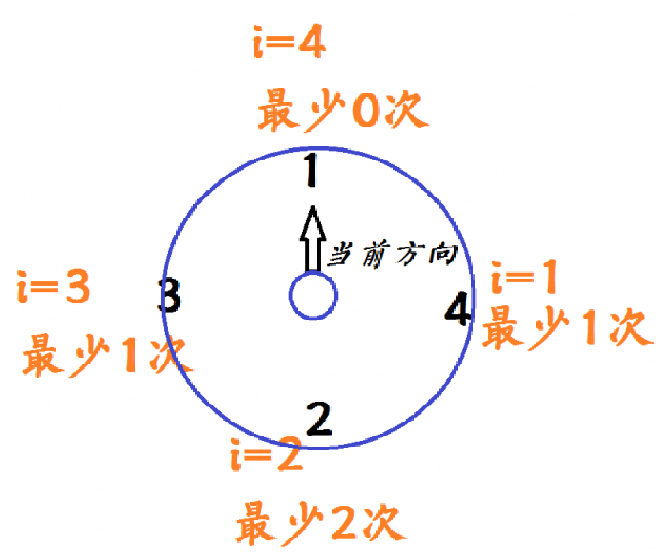
int abc[5]={0,1,2,1,0};

当i=4，最少0次；当i=3，最少1次；当i=2，最少2次；当i=1,最少1次

不难看出当对于不同的i，也就是顺时针转动i次时，对应的最小旋转次数就是abc[i]。

ft数组

1
int ft[5]={0,1,4,2,3};

img

图中蓝圈内四个方向各有一个黑色数字代表方向编号，那么我们顺时针遍历一下就是1 4 2 3，是比较好理解的。

BFS状态转移方程

边界处理，因为机器人是有体积的，而我们是将其右上角当成其位置进行广搜，所以要保证：

1
(x>=1&&x<n&&y>=1&&y<m)

代码细节

用队列存储每一个格点的信息，然后起点入队，每次从队首取出一个元素，根据这个元素旋转，直行，得到一个新的坐标，然后判断由这种方式到达的这个点是否是耗时最短的一种方式，此处用f[i][j]数组表示，然后队列为空后，输出f[终点的x][终点的y]即可。

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
#include<bits/stdc++.h>

using namespace std;
int sd[55][55];
int a[55][55];//a为读入的方格地图 
int n, m;
int x11, y11;//起点 
int x2, y2;//终点 
int f[55][55];//f为格点地图 
int fx[5] = {0, -1, 1, 0, 0};//fx[i]表方向i(编号)的x情况  
int fy[5] = {0, 0, 0, -1, 1};//fy[i]表方向i(编号)的y情况 
int ft[5] = {0, 1, 4, 2, 3};//ft[i]表示顺时针排列各个方向的编号(上1 右4 下2 左3) 
int fft[5] = {0, 1, 3, 4, 2};//fft[i]表示数字i在ft[]数组中的下标 

int abc[5] = {0, 1, 2, 1, 0};//abc[5]表示转到[顺时针转i次到达的那个方向]的最短次数 
struct node {
    int x, y;//机器人当前点的坐标 
    int t;//1=>N 2=>S 3=>W 4=>E 题目里的方向编号 
    int time;//从起点到当前点的最短时间 
};

queue<node> q;//这是队列q 
string ch;//这是读入起点的方向 
int cto;//这是起点的方向 

void fxto() {
    switch (ch[0]) {
        case 'N':
            cto = 1;
            break;
        case 'S':
            cto = 2;
            break;
        case 'W':
            cto = 3;
            break;
        case 'E':
            cto = 4;
            break;
    }
    return;
}

void change() {
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            if (sd[i][j] == 1)//如果当前格为障碍物，则它的四个顶点都不能走 
            {
                a[i - 1][j] = 1;
                a[i][j - 1] = 1;
                a[i - 1][j - 1] = 1;
                a[i][j] = 1;
            }
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            scanf("%d", &sd[i][j]);
        }
    }
    cin >> x11 >> y11 >> x2 >> y2;
    cin >> ch;
    fxto();//判断ch代表的方向 
    change();//把方格地图转化为机器人可以走的格点地图 
    node first;//起点 
    first.x = x11;
    first.y = y11;
    first.t = cto;
    first.time = 0;
    q.push(first);//起点入队 
    node u, d;
    while (!q.empty()) {
        u = q.front();
        q.pop();
        for (int i = 1; i <= 4; ++i) {
            int zhuan = abc[i];//[顺时针转i下的那个方向]的最短旋转次数 

            //求出旋转完了以后方向的编号fangx(为了方便讨论，全部当做顺时针旋转) 
            int fangx = fft[u.t] + i;//此时fangx为下标 
            if (fangx == 5) fangx = 1;
            if (fangx == 6) fangx = 2;
            if (fangx == 7) fangx = 3;
            if (fangx == 8) fangx = 4;
            fangx = ft[fangx];//此时fangx为方向编号 
            //此时fangx存的是由当前点顺时针转了i次后到达的方向的编号

            for (int j = 1; j <= 3; ++j)//走1~3步 
            {
                int lsx = u.x + fx[fangx] * j;//计算按当前旋转方向走j步的坐标 
                int lsy = u.y + fy[fangx] * j;
                if (lsx >= n || lsx <= 0 || lsy >= m || lsy <= 0 || (lsx == x11 && lsy == y11) || a[lsx][lsy] == 1) {
                    //判断边界和障碍物 (特判：是否为起点)
                    break;
                }
                if ((u.time + zhuan + 1 < f[u.x + fx[fangx] * j][u.y + fy[fangx] * j] ||
                     f[u.x + fx[fangx] * j][u.y + fy[fangx] * j] == 0) &&
                    a[u.x + fx[fangx] * j][u.y + fy[fangx] * j] == 0) {//如果当前点可以刷新距离，就入队 
                    d.x = u.x + fx[fangx] * j;
                    d.y = u.y + fy[fangx] * j;
                    d.t = fangx;
                    d.time = u.time + zhuan + 1;
                    f[u.x + fx[fangx] * j][u.y + fy[fangx] * j] = d.time;
                    q.push(d);
                }
            }
        }
    }
    if (f[x2][y2] == 0 && (x2 != x11 || y2 != y11))//如果为0，代表不能走到 
    {
        cout << "-1" << endl;
    } else//否则输出终点的距离 
        cout << f[x2][y2] << endl;
    return 0;
}